- Published on
Leetcode 203 - Remove Linked List Elements
Hello there! Today we will continue our journey into linked lists with Leetcode 203 - Remove Linked List Elements. This is a quite common question to solve with regards to efficiently removing nodes from a linked list.
Problem statement and analysis
As always, let's take a look at the problem description for this algorithm:
Given the head of a linked list and an integer val, remove all the nodes of the linked list that has Node.val == val, and return the new head.
So starting out suppose we have a linked list as such:
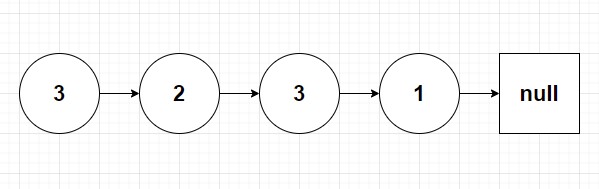
We want remove all nodes with the value of 2. How might we go about doing this using previous methods we have used when looking at linked list solutions? If you guessed two pointer method you are correct 🙌. So let's look at the psuedocode for removing the node with value of 2 in the above list.
// initialize prev pointer to null
// initialize curr pointer to the head node
// loop while curr point is not null (reached end of linked list)
// if curr is pointing to a node containing the targetted value
// set node pointed to by prev's next pointer to the curr node pointers next
// otherwise set the prev point to be the curr pointer
// set the curr pointer to be the next node it points to
// end loop
// return head
So visually if we apply this psuedocode to our diagram we get something like this:
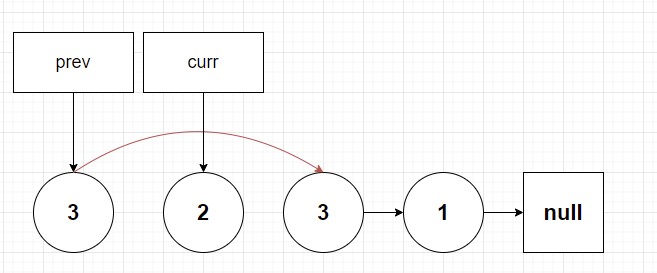
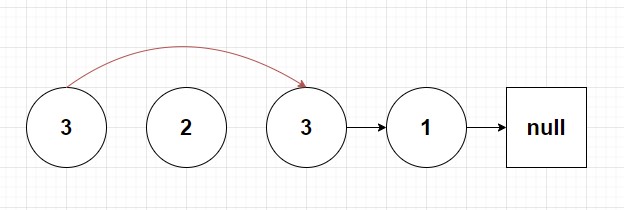
Too easy right? So you might ask, "Paul why is this problem difficult? And why are you not showing me the corresponding typescript code and telling me to have a nice journey learning about algorithms"? 🤔 Well as with all of these linked list problems there's always a catch. Let now examine what I call case 2, where one of the nodes that needs to be removed is at the head of the linked list.
So taking the same linked list as above lets now remove all node with the value of 3 from the linked list. Do you already spot the problem? Take a second ⌛ and looking at the above psuedocode on paper draw out how you might remove the head node. It turns out to be a trick question and here is why. Recall the if condition inside our loop iterating through the linked list:
// if curr is pointing to a node containing the targetted value
// set node pointed to by prev's next pointer to the curr node pointers next
At the start of iterating through our linked list what have we initialized prev pointer to? null. Well it's very hard to assign the next pointer to a node that is in fact not a node at all and is null. 🤯
// TypeError: Cannot read property 'next' of null
Now to be honest at this point I actually got stuck. I considered creating a new condition to check to see if the first node of the list's value matched the target value:
if (prev === null && curr.val === target) {
curr = curr.next;
}
But sadly this does not work because actually all you have done is iterated down the list one more value. And in fact when you return the head node the list doesn't change at all. Fundamentally this is because without the prev pointer to "bypass" the head node we have not actually removed the node at all!
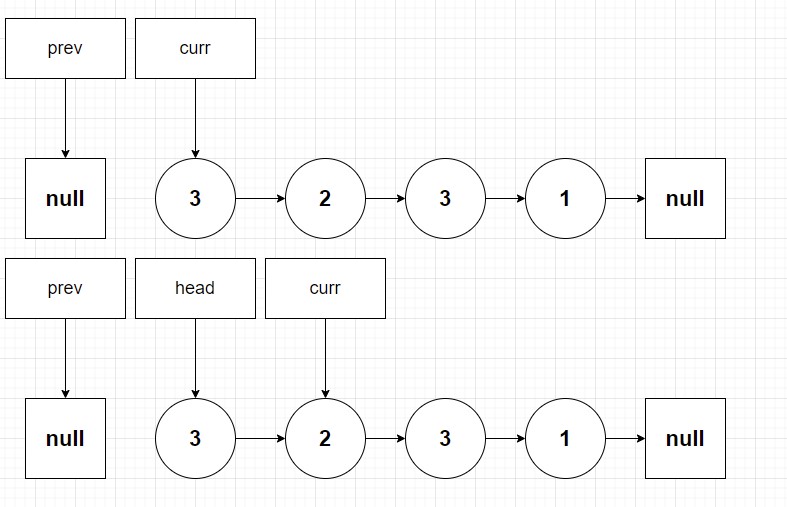
So at this point an inversion of thinking we so often have when solving algorithms is required. Removing a node is really, REALLY easy when it's between two other nodes. Wouldn't it be cool if we could guarantee that every time we need to remove a node it is always between two other nodes? Well it turns out that it's quite simple to do this through the concept of the sentinel node.
The sentinel node is just a fancy way of saying let's put a dummy node in front of the linked list in order to guarantee that all nodes can use our previous psuedocode algorithm. Confused? That's okay, let's take a look at a diagram:
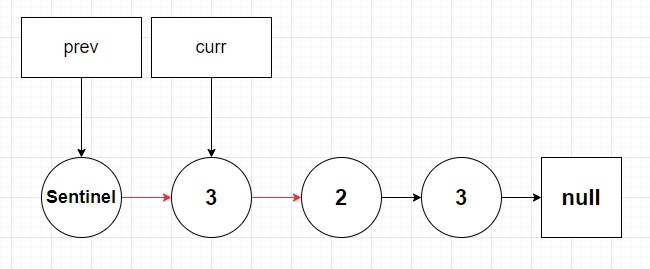
Instead of initializing our prev pointer to null we now point it to the sentinel node. Can you now see how this is useful to solving our head node problem? Let's take a look visually:
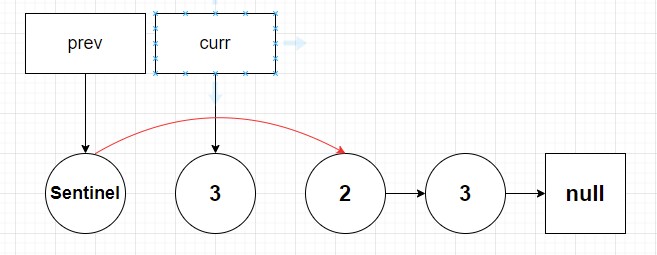
So by now having this sentinel node we have eliminated the type error we previously saw because we never have the case of prev ever starting as null. Rather it's always a node with no val pointing to the head node. So after this small change all nodes in the list can be treated as nodes we previously looked at. Finally, instead of returning the head node once we are done we return the sentinel node's next pointer. We must do this because if we remove the head node in the case it contains the target value it would be null and thus we would otherwise incorrectly return a null linked list.
So here is our final solution!
/**
* Definition for singly-linked list.
* class ListNode {
* val: number
* next: ListNode | null
* constructor(val?: number, next?: ListNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
* }
*/
function removeElements(head: ListNode | null, val: number): ListNode | null {
if (!head) return head;
const sentinel = new ListNode();
sentinel.next = head;
let prev = sentinel,
curr = head;
while (curr !== null) {
if (curr.val === val) {
prev.next = curr.next;
} else {
prev = curr;
}
curr = curr.next;
}
return sentinel.next;
}
Complexity analysis
Wew that was a fun one. But what is our complexity with this solution? Well just like most other link list problems we have to navigate through the entire list at minimum once in order to find any nodes that match the target value. In the above algorithm we have one while loop that traverses the entire list. Thus our computational complexity turns out to be O(N). Now what about space complexity? Well we end up needing one additional list node and two pointers to solve this problem. But this quantity does not scale with the size of the linked list. Thus space complexity becomes O(1).
Thank you as always and best of luck with your journey with algorithms!
