- Published on
Leetcode 141 - Linked List Cycle
After a rash of string and array problems I thought we would take a break today and start discussing linked lists. To start out let's take a closer look at Leetcode 141 - Linked List Cycle
I will start this solution by assuming the reader understands the basics of a linked list and its implementation. If not that's okay. There are a wealth of resources on the topic (and I plan to cover this in the near future with my own implementation). But for now please go review resources (I recommend this) and feel free to come back one you've had a chance to learn/brush up.
As always let's look at the problem being asked:
Problem statement and analysis
Given head, the head of a linked list, determine if the linked list has a cycle in it. There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Return true if there is a cycle in the linked list. Otherwise, return false.
Alright so some concepts are being throw out here. What exactly does a cycle mean in plain words? Well often a picture is 1000 words so lets take a look at one here:
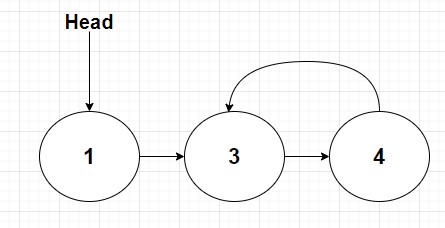
What we see here is that a linked list of size 3 is initialized. Starting at the head we point to a node containing the number 3. This node then points to another node containing the number 4. Now normally we would expect the end of the linked list to point to null, or the absense of a node. However in this case we follow the diagram and note that the final node points back to node 3. So in this case what we see is that as we traverse the linked list we will continue to rotate between nodes containing the values and 3 and 4. And thus a cycle is found.
Now that we understand the formal defintion of what a cycle is how might be go about figuring out if a given linked list contains a cycle? We will look at two approaches here, one theoretically and one with a formal code solution.
Approaches and solutions
Approach 1: Hash Table
If you mind initially went to hashing as you read the problem statement then the good news is you were correct! This is absolutely a viable approach to solving this problem! So what might hashing look like in this scenario? Let's look at a quick psuedocode solution:
// check whether list is less than or equal to length 1.
// If it is then return false because it's imposible to have a cycle
// otherwise initialize a set
// loop while head is not null
// check to see if set contains this node
// if it does, then we have found a cycle, return true
// otherwise we haven't seen this node yet, add it to our hash table
// set head to be next node it is pointing to.
// if we reach the end of the loop then we did not find a cycle
// return false
Seems pretty straightforward and very similar to array problems we have worked previously. Basically if we come across the same node twice while looping through the linked list then we have found a cycle. From a complexity perspect we are at O(N), where N is the length of the entire linked list because intuitively we must always traverse the entire linked list to ensure whether there is actually a cycle or not. Space wise we also reach O(N) since the hash table similarly grows with the length of the list.
However there is a much simpler O(1) memory approach we can take. Let's now review the infamous Floyd's Cycle Finding Algorith.
Approach 2: Floyd's Cycle Finding Algorith
This is actually a quite fascinating variation of the two pointer method that is used for many algorithms. Rather than maintaining a hash table of tracked nodes we initialize 2 additional pointers. One pointer is going to navigate the linked list slowly, or that is to say 1 node at a time 🐢. Another pointer moves twice as fast (2 nodes at a time) 🐇. How does this help us exactly?
Well imagine we are at a Nascar race (racing in loops for our F1 fans out there). Let's assume one car is racing at 50 mph. Another car has a much better day and is riding at 100mph. If both cars start at the same part of track when the faster car finishes a lap, the slower car is roughly halfway around the loop. The slow and fast car then meet again by the end of the track.
So how does this apply to linked list cycles? Well simply put in a normal linked list the fast pointer should fall off the list and always be null. The slow pointer eventually becomes null after N iterations. But in the case of a cycle the fast pointer will come back around. If we offset the fast ptr by 1 with respect to the slow pointer the only way the slow and fast pointer could possibly point to the same node is if there is in fact a cycle! Alright let's look at the solution code:
// Definition for singly-linked list.
// class ListNode {
// val: number
// next: ListNode | null
// constructor(val?: number, next?: ListNode | null) {
// this.val = (val===undefined ? 0 : val)
// this.next = (next===undefined ? null : next)
// }
// }
function hasCycle(head: ListNode | null): boolean {
//base cases
if (!head || head.next === null) return false;
//set 2 pointers 2 apart
let ptra = head,
ptrb = head;
while (ptrb.next !== null) {
ptra = ptra.next;
ptrb = ptrb?.next?.next;
if (ptra === ptrb) return true;
}
return false;
}
So this solution should look pretty similar to the first solution. We first do a base case check to see whether we can easily determine whether the list can never have a cycle. We then initialize 2 pointers and start looping through the list. Before comparing the pointers we move the slow pointer by one node and the fast pointer by two nodes. If the fast and slow pointer match we have found a cycle. Otherwise if the fast pointer is null then we know there are no cycles.
You might ask why we don't check the slow pointer in our loop. The reason it is unecessary is because even though the fast pointer moves faster than the slow pointer they both operate on the same linked list. Thus if the fast pointer hits null then the slow pointer will also hit null eventually and thus we can reduce the average case time.
Completity wise we still remain at O(N). This is because even with two pointers we still could find the cycle at the very end of the linked list. However from a space perspective we have added 2 simple pointers which does not increase in quantity with the linked list size. Thus we now have reduced space complexity to O(1).
Thank you so much as always and best of luck exploring linked lists!
