- Published on
Leetcode 121. Best Time to Buy and Sell Stock (JavaScript)
It's time to mix an array problem with some light dynamic programming in LeetCode 121 - Find Numbers with Even Number of Digits
Problem statement and analysis
Let's start by taking a look at the problem statement:
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
An example is given of:
Input: prices = [7,1,5,3,6,4]
Output: 5and
Input: prices = [7,6,4,3,1]
Output: 0So what is really the ask here? What the problem succinctly is trying to tell us is to figure out how to make the most money by buying and selling a stock only once. If there's no chance we can make a profit then we should should not to buy/sell at all. In reality what we are trying to do simply find the maximum positive delta between two numbers that are in increasing order.
Approach One - Brute Force
The intuitive approach to this problem is of course the brute force solution. In other words for each number (in order) in the array we look one by one and determine what the maximum positive delta for each number. The maximum of these instances is our max profit. Let's review some quick psuedocode:
// For every number in the list
// For the rest of the numbers after this number in the list
// Take the difference of the inner loop number and the first loop's number
// If this difference is larger than the previous "largest" difference, update the largest differenceComplexity is pretty straightfoward for this one. We have 2 nested for loops. Therefore computational complexity is O(N^2). Space complexity is O(1) because we just use a variable or two to store intermidate values (which does not scale with the input size).
Approach 2 - Dynamic programming
For the second approach we are going to do a little light dynamic programming. It turns out there is actually a single loop approach to this problem. We are going to slowly start delving into the concept of dynamic programming as we begin to solve more leetcode problems. But essentially today what we want to use is a technique called "the greedy approach". Let's look at a quick plot of the first example that was provided.
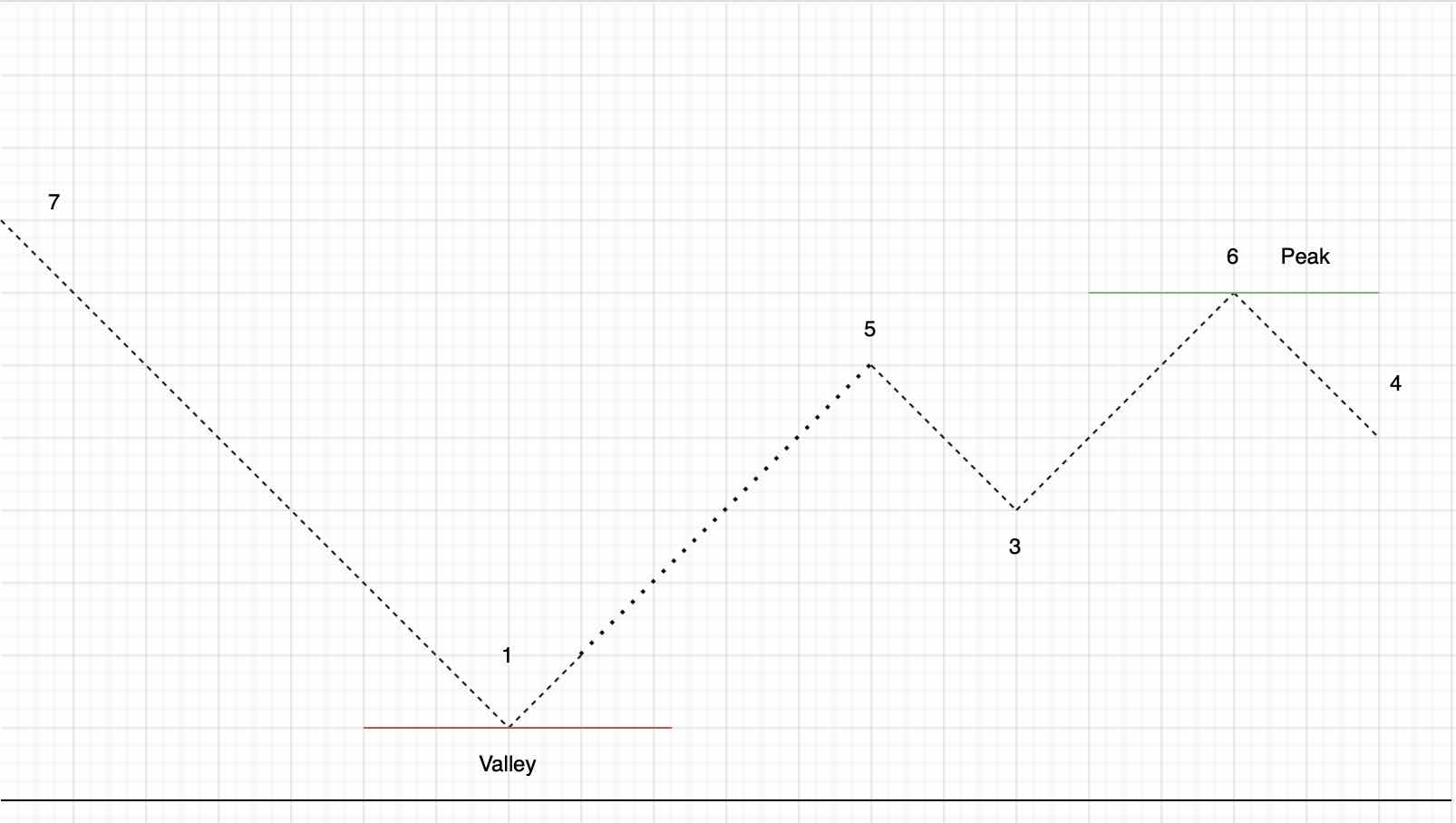
Did this help to understand what the one approach solution is? So as we scan across this peak and valley chart we observe local minima and maxima and an absolute minima and maxima (highlighted via text and also a line).
The largest maxmia after the smallest minima is the largest delta (or profit) we can derive for a given list of stock prices. And this is exactly what we will do. We will go through numbers one by calculating the largest delta (profit) so far by examining the deltas between stock prices. But unlike approach number 1 we are not going to rotate all permutations for every number in the stock list. Instead we are going to compare the maximum profit calculated so far to maximum profit for each number in the list (using the minimum value we have found so far from previous iteration).
Confused? That's okay! What we are doing above is the aforementioned "greedy" approach. In other words if the next value in the list increases our profit as we iterate we take it immediately. Any localized profit that exceeds our overall maximum profit so far becomes our new maximum profit. If the next stock lowers the localized profit (but does not cause to go negative) we simply continue as it is possible that the next number in the list could be larger than the current stock price resulting in a new maximum profit. If the stock price we are looking at is lower than anything we have detected before it becomes our new absolute minima and we move onto the next price.
Okay with all those words out of the way let's look at some psuedocode
// for each price in the stock list
// check to see if the number is the new lowest stock price
// if it is, that our new absolute minima, move on
// else check if this stock price minus the absolute minima is our new largest profit
// if it is, set maximum profit to this number.
Hopefully we are a little clearer than mud now on the algorithm. The completed code is as follows:
function maxProfit(prices: number[]): number {
let maxProfit = 0;
let minPrice = Number.MAX_SAFE_INTEGER;
//base case
if (prices.length < 2) return maxProfit;
for (let i = 0; i < prices.length; i++) {
if (prices[i] < minPrice) {
minPrice = prices[i];
} else if (prices[i] - minPrice > maxProfit) {
maxProfit = prices[i] - minPrice;
}
}
return maxProfit;
}
Complexity analysis is thankfully pretty straightforward here. We have one single loop which gives us a nice computational complexity of O(N). Space once again is O(1) as we use a few temporary variables that does not scale with stock price list size.
As always thank you and best of luck with your algorithmic journey!
